Exploring SIMD

Support for Single-Instruction-Multiple-Data (SIMD) will be added in C++26. An experimental implementation of the proposed SIMD library has been available in gcc since version 11. In this post we are going to explore the library and run some benchmark tests.

As always the code is available from GitHub.

Some history

The ability to perform the same operation on multiple data points simultaneously is not new to the computing world and goes back as far as 1966. Streaming SIMD Extensions (SSE) to x86 architecture were introduced by Intel in 1999. It quickly found its use in digital signal processing and scientific applications. For many years the computing landscape was dominated by Intel and their Integrated Performance Primitives (IPP) library was a de-facto standard in bringing the power of SIMD to your application.

In the recent years the situation has changed (and not in Intel’s favour). There are many more players on the CPU market now with AMD going from strengths to strengths, AWS heavily investing in chips for cloud computing and Apple designing and building their own processors. At the same time compilers became much better at utilizing SIMD on the supported platforms.

Having SIMD support as part of the standard C++ library is great news for every software engineer developing portable and computationally extensive applications. To be successful though it needs to hold its “zero overhead” promise (meaning that you don’t pay for features that you don’t use) and be easy to use.

Using std::experimental::simd

If you are using gcc version 11 or above all you need to unleash the power of SIMD is to #include <experimental/simd>. Well, almost. The library provides a template container native_simd for storing multiple data points for simultaneous processing. As signal processing engineers we are mostly interested in single precision floating point data, so we will be using native_simd<float>. To find out how many data points fit in this data type on your architecture you can use native_simd<float>::size. Two methods copy_to and copy_from are provided to pack and unpack data to and from the native_simd container. All arithmetic operators and most of standard functions from the <algorithms> library were overloaded to support native_simd.

Here is an example of a helper function to load data to a vector of native_simd<float>:

namespace stdx = std::experimental;
inline void copy_to(const float *src, size_t src_size, std::vector<stdx::native_simd<float>> &dst)
{
    const size_t w = stdx::native_simd<float>::size();
    assert(src_size % w == 0);
    const size_t num = src_size / w;
    dst.resize(num);
    auto p = src;
    for (size_t k = 0; k < num; ++k)
    {
        dst[k].copy_from(p, stdx::vector_aligned); // or stdx::element_aligned
        p += w;
    }
}

With the data packed, it could be processed as usual. For example, to add two vectors x and y and store the result in vector z we use:

for (size_t k=0; k < z.size(); ++k)
{
    z[k] = x[k] + y[k];
}

If you are familiar with CUDA programming you might think of native_simd as “device memory”.

Benchmarking Performance

Accurate benchmarking of SIMD implementation is well beyond the scope of this blog. For our purposes it suffices to compare three implementations: a straightforward loop, IPP functions and std::experimental::simd.

Our test problem consists in updating the values of three vectors containing 1000 elements each. The first two vectors x and y contain uniformly distributed numbers in the range from 0 to 1. At each update every element of x and y are multiplied by two constants alpha and beta. Vector z accumulates the sum of squared elements:

for (size_t k = 0; k < z.size(); ++k)
{
    x[k] *= alpha;
    y[k] *= beta;
    z[k] += x[k] * x[k] + y[k] * y[k];
}

Initially, all elements of z are zeros. The update operation is repeated 10000 times. The results of the calculations were compared between three implementations to test for correctness and prevent the compiler from optimizing out the code.

IPP implementation replaces the loop with four function calls:

ippsMulC_32f_I(alpha, x.data(), x.size());
ippsMulC_32f_I(beta, y.data(), y.size());
ippsAddProduct_32f(x.data(), x.data(), z.data(), x.size());
ippsAddProduct_32f(y.data(), y.data(), z.data(), y.size());

In this case, x, y and z are custom IPP buffer types that wrap ippMalloc and ippFree functions using RAII method. The allocated buffers are guaranteed to be properly aligned in memory thus stdx::vector_aligned flag can be safely used when calling copy_to and copy_from methods.

The implementation that uses std::experimental::simd is identical to the loop implementation except that x, y and z are of type native_simd<float>

The code was compiled with gcc version 14.1.0 using flags “-O3 -march=native”. The test platform was a Lenovo T430 desktop with Intel(R) Core(TM) i7-3520M CPU .

Results

The execution time for the three implementation is shown in the figure below.

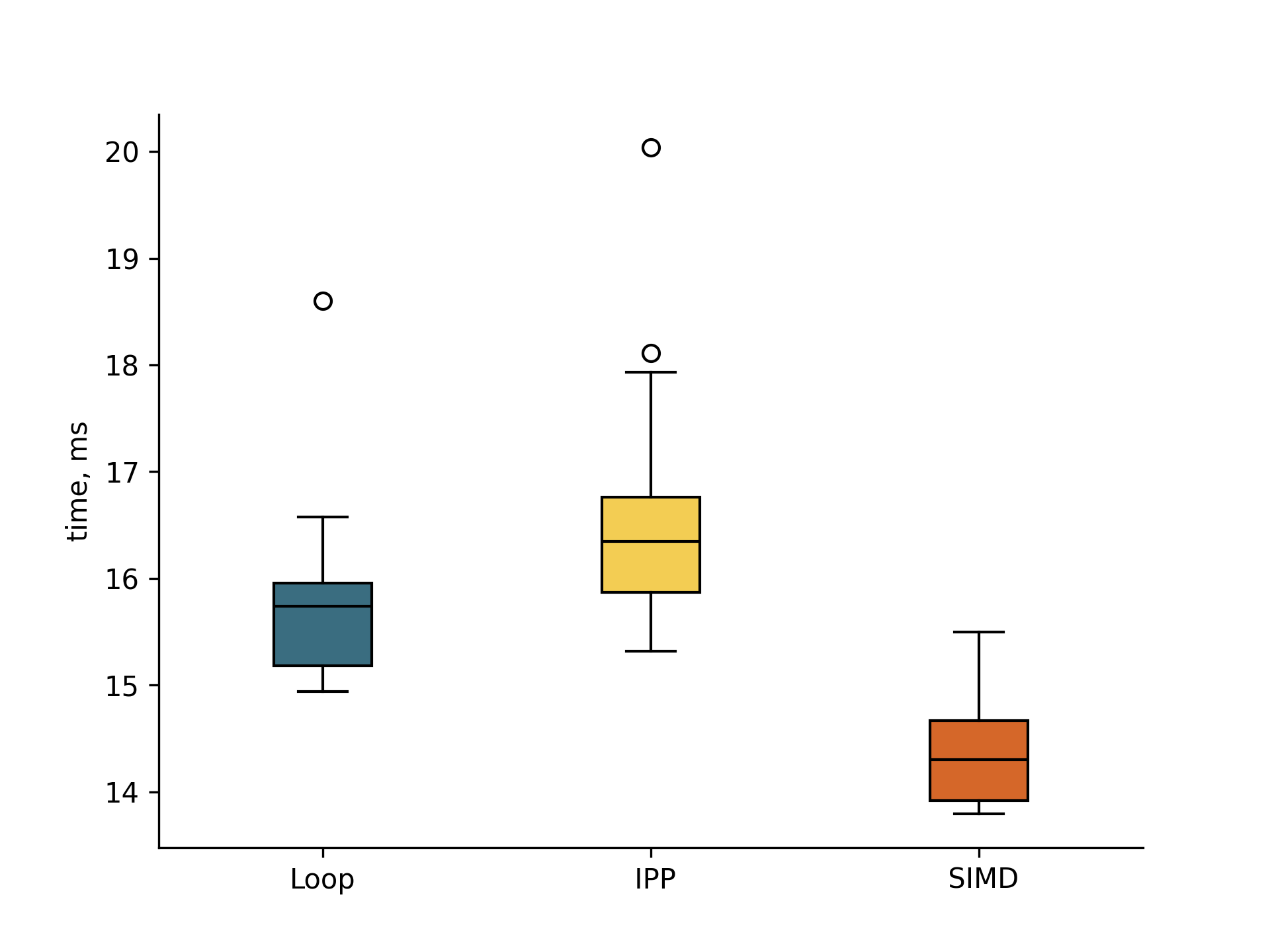
The results are exactly opposite to what I expected. Surprisingly, Intel IPP demonstrates the worst performance 4% below the baseline implementation. gcc compiler on the other hand made a very good job optimizing the code. std::simd is a clear winner with 10% increase in performance. While small, the difference is significant considering that the problem is most likely memory-bound.

Another important finding is that IPP output was not identical to the other two methods. The errors were quite large (minimum: -0.00016; maximum: 0.0035; mean: 0.00054) and could indicate a serious problem in the implementation. This warrants further investigation.

Conclusion

The new std::simd library exceeded my expectations both in terms of performance and ease of use. The small overhead of packing and unpacking data to and from native_simd type is unlikely to affect most computationally extensive applications. A few small utility functions hide the complexity of using this SIMD container and increase code safety.

Another pleasant surprise came from gcc with its excellent code optimization performance. If you develop an application to run on a specified hardware (which is often the case in industrial applications) it is worth experimenting with gcc to achieve the best performance.

I used IPP for more than a decade and always took its performance and correctness for granted. This simple exercise reminded me of the importance of profiling, benchmarking and testing. The difference in the results obtained from IPP and the baseline implementation were particularly alarming.