Object Oriented Programming (OOP) and Data Oriented Design (DOD) are two radically different approaches to building software. In this blog post we illustrate both methods, introduce a middle-ground solution and represent the results of performance benchmarks.

OOP models the program behaviour through a set of objects which contain (encapsulate) relevant data and interact through calling each other methods. OOP has been the main methodology for several decades, it is well understood and widely used. The approach is criticized for its multiple levels of abstractions that makes it hard to reason about the code, bloated code bases, difficulties with testing, and most importantly, poor performance due to the overhead introduced by virtual function calls and low data proximity.

DOD, on the other hand focuses on the data flow in the program and builds the architecture around the data. It tends to use simple data containers and employs several techniques to avoid costly virtual functions relying on much more flexible function polymorphism, templates and other tools available in modern C++.

We are not going to descend into heated debates about the advantages of one approach over the other. As “C++ programmers in the trenches” we are primarily concerned with:

• performance of our code;
• code complexity, and
• maintainability.

Thus, let us implement both approaches and compare them based on these criteria. To keep things simple we will use the classic example of geometry shapes, the “Hello world” of the OOP.

The code is available on GitHub.

The method

We will implement a simple problem. We are given an array consisting of circles and rectangles. We need to implement a transformation consisting in translating the origin of each shape by a certain distance in the x and y coordinates, change the colour to a specified value and calculate the sum of all areas in the array. This accomplished, we can measure the time required to apply this transform to a large array of randomly initialised shapes and assess the implementations for code complexity and maintainability.

OOP solution

Since this is a textbook example, let us just look at the code.

struct basic_shape
{
    point origin;
    shape_color color{default_color};
    basic_shape(const point &o, const shape_color &c)
        : origin{o}, color{c}
    {
    }
    virtual float area() const { return 0; }
    virtual ~basic_shape() = default;
};

struct circle : public basic_shape
{
    float radius{0};
    circle(const point &o, const shape_color &c, float r)
        : basic_shape{o, c}, radius{r}
    {
    }
    float area() const override final { return 3.1415926535f * radius * radius; }
};

struct rectangle : public basic_shape
{
    float a{0};
    float b{0};
    rectangle(const point &o, const shape_color &c, float side_a, float side_b)
        : basic_shape{o, c}, a{side_a}, b{side_b}
    {
    }
    float area() const override final { return a * b; }
};

The point class is a struct containing x and y fields of type float. The shape_color is an alias for std::array<char, 4> and stores the colour of the shape in the RGBA format.

The constructors for the circle and rectangle classes are not strictly required, but they are handy if we want to construct the objects using initialization lists. As long as we remember to define a virtual destructor for the base class, we are good to go.

DOD solution

Following the DOD principles we keep similar data together. If, for example, we decide to select and translate all the shapes in our hypothetical scene we would need to access only the origins vector thus maximising the memory bandwidth and cache utilization.

Likewise, the circles and rectangles are represented by the vector of radii and sizes, respectively. It might be a good idea to define a radius type as an alias for float to improve readability.

struct shape_size
{
    float width{0};
    float height{0};
};

typedef float radius;

struct shapes
{
    std::vector<point> origins;
    std::vector<shape_color> colors;
    std::vector<radius> circles;
    std::vector<shape_size> rectangles;
};

Tagged Union

An attentive reader would probably wonder if there is a way to avoid the OOP boilerplate and at the same time have something a bit more expressive than vectors of numbers in the DOD solution. A compromise does exist in the form of a tagged union or std::variant that was introduced in C++17.

In case you are unfamiliar with unions, it is a special type of class that can hold one of several types of data members at any time. The memory is allocated to store the largest type in the union, so some memory will inevitably be wasted if the data types differ in size a lot.

The trick is to store a tag in the union that would identify which type is stored at runtime. This is a totally valid C++ code since accessing the member function from a different type does not cause undefined behaviour as long as the memory layouts of the types coincide.

For example, if the following tagged union is defined as:

union tagged
{
    char tag{0};
    struct
    {
        char tag{char(1)};
        float radius{0};
    } circle;
    struct
    {
        char tag{char(2)};
        float width{0};
        float height{0};
    } rectangle;
};

it can hold either a tag of type char, a circle or a rectangle. Provided we start each shape structure definition with char tag; we can use it as follows:

std::vector<tagged> v = {tagged.circle{}, tagged.rectangle{}};
for (const auto &x:v)
{
    if (x.tag == 1)
    {
        std::cout << "circle\n";
    }
    else
    {
        std::cout << "rectangle\n";
    }
}

The tagged union can now be used inside a structure that stores common fields for the circles and rectangles:

enum class shape_tag {none, circle, rectangle};

struct shape
{
    point origin;
    shape_color color{default_color};
    shape_tag tag{shape_tag::none};
    union
    {
        radius circle;
        shape_size rectangle;
    };

    shape(const point &xy, const shape_color &c, float r)
        : origin{xy.x, xy.y}, color{c}, tag{shape_tag::circle}, circle{r}
    {
    }

    shape(const point &xy, const shape_color &c, float a, float b)
        : origin{xy.x, xy.y}, color{c}, tag(shape_tag::rectangle), rectangle{a, b}
    {
    }
};

std::variant

std::variant has been part of the standard library since C++17. The implementation is similar to the tagged union except that it uses templates and the std::visit function to access the content stored in the variant.

The implementation for storing circles and rectangles can look like this:

struct circle
{
    point origin;
    shape_color color{default_color};
    float radius{0};
};
struct rectangle
{
    point origin;
    shape_color color{default_color};
    float a{0};
    float b{0};
};

using shape = std::variant<circle, rectangle>;

Accessing the shapes involves some template magic:

double area(const shape& s)
{
    return std::visit([](auto &arg) -> double
                                 {  using T = std::decay_t<decltype(arg)>;
                                    if constexpr(std::is_same_v<T, circle>)
                                    {
                                        return 3.1415926535 * arg.radius * arg.radius;
                                    }
                                    else if constexpr(std::is_same_v<T, rectangle>)
                                    {
                                        return arg.a * arg.b;
                                    }
                                    else
                                    {
                                        return -1;
                                    } },
                                 s);
}

We need to drill down into the lambda function argument to extract its type by using std::delay<decltype(arg)>::type. The std::delay performs the type conversions equivalent to the ones performed when passing function arguments by value.

Performance

Vectors containing 500000 random elements of type circle and rectangle were generated for the OOP, Tagged Union and variant implementations using the same seed value to ensure that they contain identical data. The DOD solution was initialized in a similar fashion, once again ensuring that the data is the same.

The transformation functions were implemented that performed a translation of the shape origin by a fixed (x, y) vector, replaced the colour with a given RGBA value and calculated the total area of all elements. The time required to perform the transformation was measured for 11 runs. The box plot of the results is shown below.

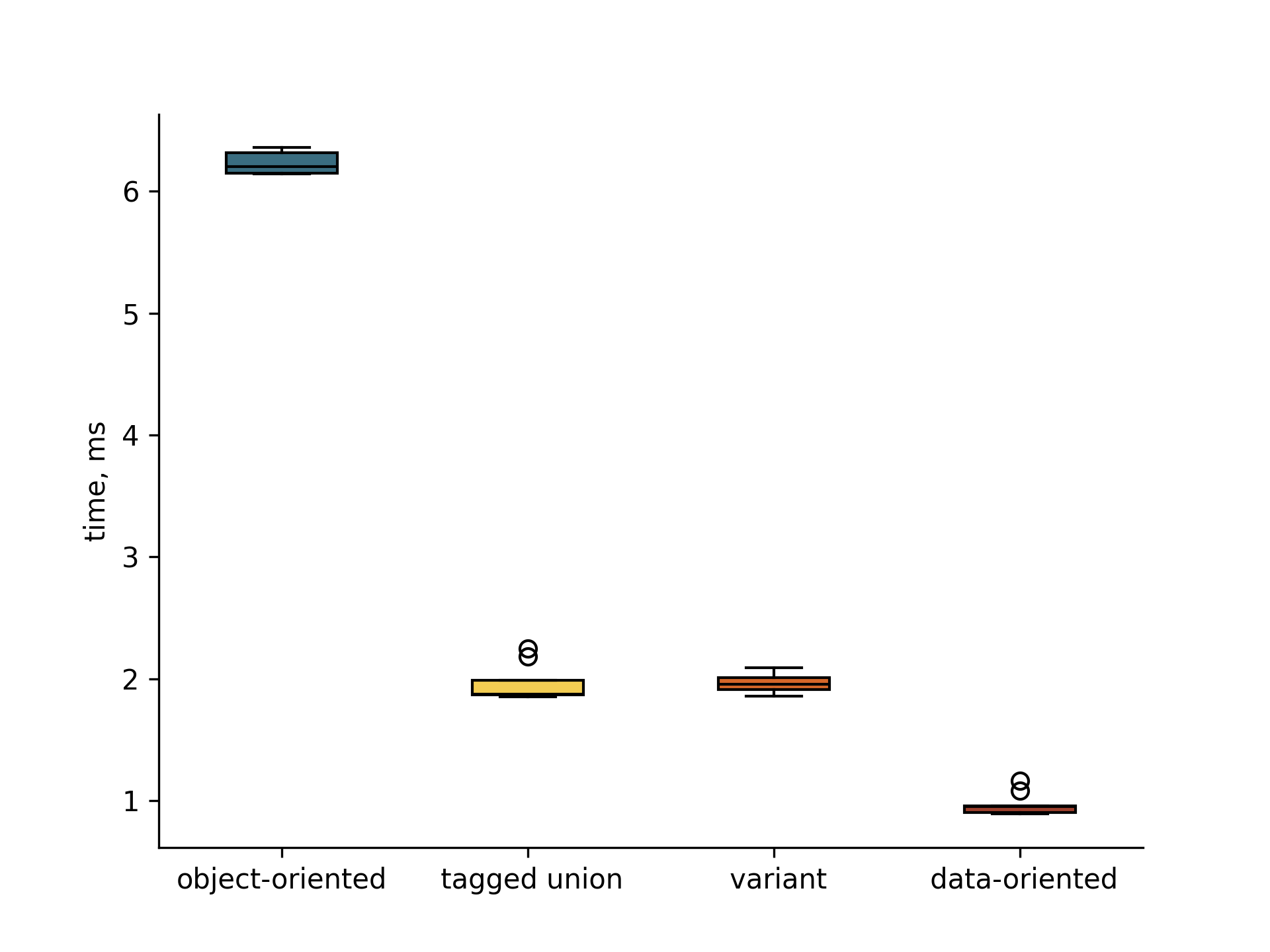
The mean speed-up achieved by replacing OOP with the other solutions is summarised in the table below.

The numbers speak for themselves. Even in our simple transformation function the combined overhead of virtual function lookup or type deduction and data spread is enormous.

Code quality

It is impossible to introduce objective metrics on the quality, readability and maintainability of code. Subjectively, object-oriented and data-oriented code are the simplest and also the shortest. Here is the OOP version:

    for (auto &s : shapes)
    {
        s->origin.x += translate_x;
        s->origin.y += translate_y;
        s->color = new_color;
        total_area += s->area();
    }

The readability of the DOD transformation code

for (auto &p : shapes.origins)
{
    p.x += translate_x;
    p.y += translate_y;
}

for (auto &c : shapes.colors)
{
    c = new_color;
}

for (const auto &r : shapes.circles)
{
    total_area += 3.1415926535f * r * r;
}

for (const auto &s : shapes.rectangles)
{
    total_area += s.width * s.height;
}

could be further improved by defining individual transforms as inline functions:

translate_origin(translate_x, translate_y, shapes.origins);
replace_color(new_color, shapes.colors);
total_area = calculate_total_area(shapes.circles) + calculate_total_area(shapes.rectangles);

To my taste, the std::variant code in its current form is the hardest to understand and maintain. Replacing the lambda function by a standalone function might somewhat improve it, though.

Conclusion

As C++ developers we care about performance. This simple experiment illustrates that the methodology you choose for your system and its architecture plays a crucial role in the performance of the application. While premature optimization is said to be the root of all evil, careful considerations for performance at the earliest stages of the design can prevent a lot of disagreeable surprises later on.

Moreover, the most performant code does not need to be ugly. Data-oriented code might look strange at first but since the concept is so simple and logical you will grow accustomed to it very quickly.

And finally, I am still ambivalent with regards to std::variant and its lower-level cousin, the tagged union. This mechanism of implementing polymorphism undoubtedly offers an advantage over OOP in terms of decoupling and performance. I can see its potential in certain scenarios like gradual refactoring of existing OOP base, but I am still cautious about recommending std::variant as the best alternative to OOP.