Optimal Solution

I saw a post on LinkedIn in which the author published his optimal solution to a coding interview problem. The challenge involved searching a sorted array. Any cheatsheet would tell you that the best solution to the problem would involve a binary search. If you are using C++ for purposes for which the language was created then you probably know that any textbook solution is suboptimal until proven otherwise. When I contacted the author of the post with a request to add benchmarks to illustrate how the optimal solution outperforms the naïve implementation I got a somewhat puzzling reply that he had no means to profile his code.

With my breakfast finished and the garden watered I certainly had time to answer my own question. Let’s start from the problem.

Problem formulation

You are given a sorted array of integers where every element appears exactly K times, except for one element that appears fewer than K times. Your task is to find the element that occurs fewer than K times.

Example

Array: [1, 1, 1, 5, 5, 5, 7, 7, 9, 9, 9, 10, 10, 10]
K = 3
Answer: 7

Analysis

As the author mentioned the first idea that springs to mind is to use a map to count elements. Then you realize that storing the counts is wasteful as you can discard them straight away if they are equal to K. A “brute force” approach is to iterate the vector and count each element terminating the search when the target element is found. A somewhat better strategy is to move two iterators K-1 elements apart and check for their equality, advancing them K steps afterwards. Conceptually:

    auto it0 = v.begin();
    auto it1 = it0 + k - 1;
    while (*it0 != *it1)
    {
        it0 += k;
        it1 += k;
    }

You obviously need to check for valid input, corner cases and deal with terminating the loop as in its present form it runs past the end of the array, but the idea should be obvious from this snippet.

The binary search approach consists in dividing the array (roughly) in halves, identifying the part that contains the target and repeating the process until we narrow the search window to the target element.

Performance

The big O theory suggests that the naïve approach has O(n) complexity while the optimal binary search solution is O(log n). Both methods do not use any additional memory. It is reasonable to expect that the optimal solution would beat our simple two-iterator implementation senseless, except probably for very small problem sizes.

So this was theory. The reality is the von Neumann architecture where everything is data (including your code) and x86 processors with their multiple levels of cache, slow memory access and the big scary thing called the instruction pipeline.

Benchmark

Both implementations were compiled in Release configuration with clang 15 using the default compiler flags. A random problem generator was implemented and the execution time was measured using the standard chrono library. The number of elements and the repetion K were fixed for each run and the execution time was averaged over 10000 runs.

The benchmarks were run on a Dell Latitude laptop with Intel i5-7200U CPU and 8 GB of memory running Windows 10.

Results

The execution time (in logarithmic scale) for both implementations is shown in the figure below for K=5. The dotted lines represent fitted curves with the equations: 0.439 * n ^ 0.999 and -726.406 + 642.782 * log10(n), respectively, where n is the number of unique elements in the array (the full size is random between (n-1)*K + 1 and n*K - 1).

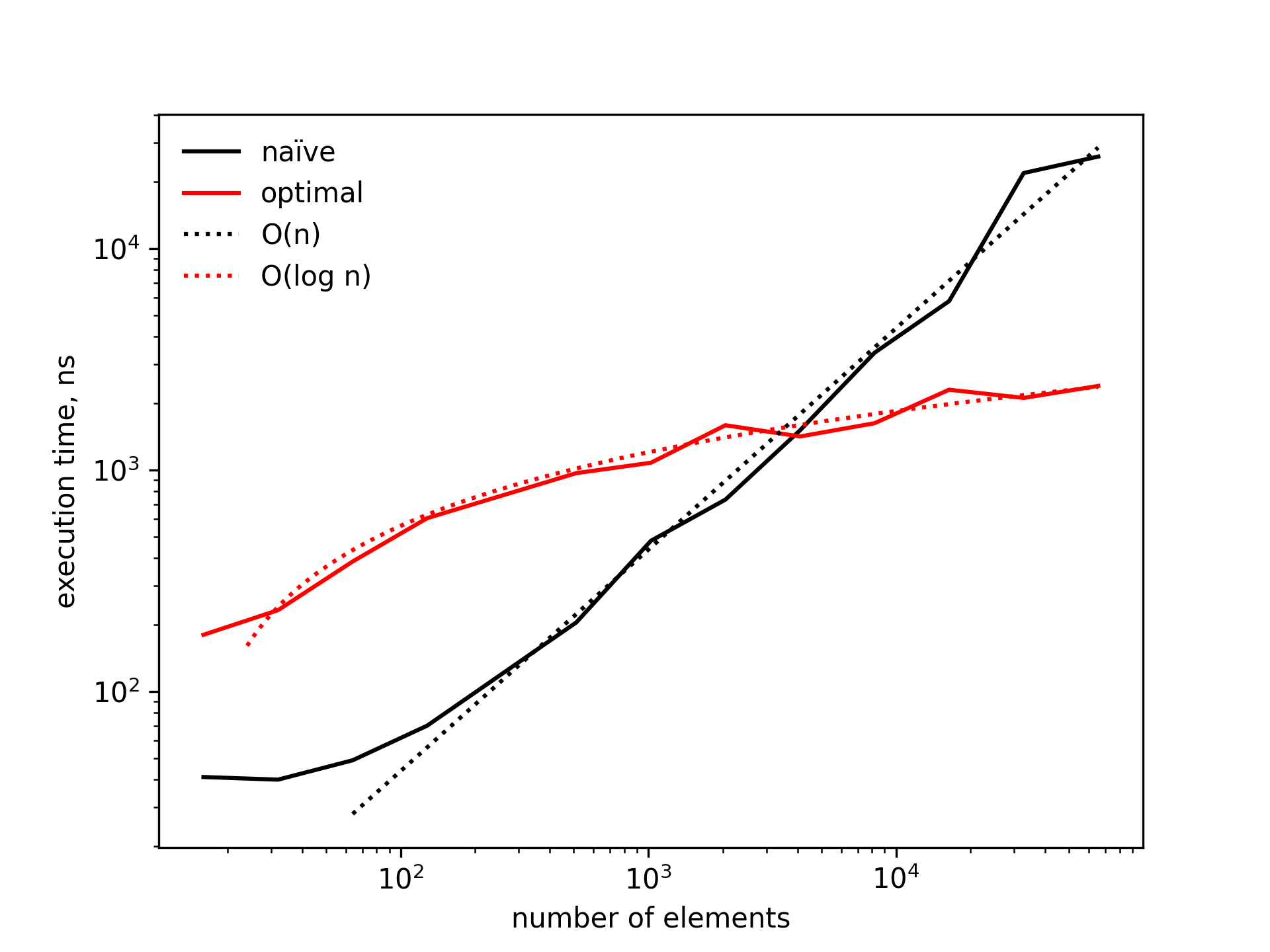
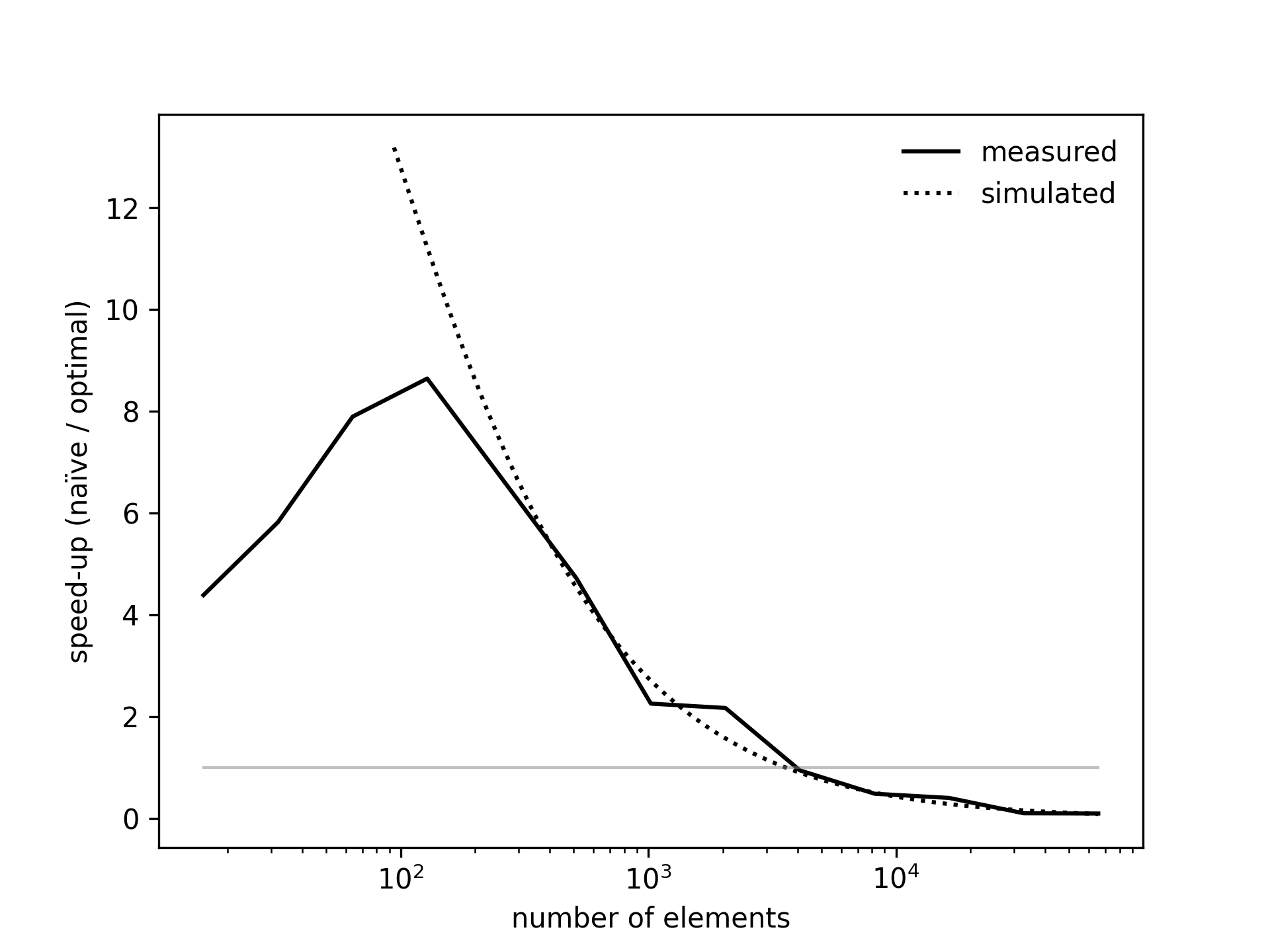
The next figure shows the ratio of execution times of the optimal vs. naïve solutions (or speed-up ratio). For relatively small problem sizes of up to 2000x5 elements the naïve algorithm outperforms its counterpart significantly, giving up to 8 times speed increase. For larger problems the situation changes, with the performance of the naïve implementation quickly falling off a cliff.

Conclusions

The main lesson that I learned from this trivial exercise is that implementation details matter. Your data and the target architecture often dictate the choice of processing algorithms and the textbook solution is rarely (if ever) the answer to the real-world problems.

If you want to experiment with the code you can find it in my GitHub respository.